List of Astronomy Equations with WorkingsUse this Astronomy Equations Cheat Sheet to help find the equations you are looking for, then see the relevant page for tutorials and how to use the equations.
This article is part of a series of articles. Please use the links below to navigate between the articles.
- Astronomy for Beginners - Complete Guide
- What are Right Ascension (RA) and Declination (Dec)?
- What is Angular Size in Astronomy?
- Magnitude Scale and Distance Modulus in Astronomy
- Sidereal Time, Civil Time and Solar Time
- What Are The Equinoxes and Solstices About?
- How Do We Measure Distance in Space Using Parallax and Parsecs
- Brightness, Luminosity and Flux of Stars Explained
- Kepler's Laws of Planetary Motion Explained
- What Are Lagrange Points?
- List of Astronomy Equations with Workings
- Glossary of Astronomy & Photographic Terms
- Astronomical Constants - Useful Constants for Astronomy
Mathematics is the engine of the universe, driving and dictating all actions, interactions and transformations. Equation-based laws underlie physical systems. Physical systems astronomers investigate include stars, planets, galaxies, gases, plasma, subatomic particles, dark matter and anything else you might find if you ventured to space.

Geometry & Trigonometry Equations
| Title | Equation | Description | Further Reading |
|---|---|---|---|
| Circle, circumference of |  Equation 1 - Circle, circumference of | Calculating the circumference of a circle. | |
| Sphere, Surface Area of |  Equation 21 - Sphere, Surface Area of | The surface area of a sphere of radius r. |
Size & Distance Equations
| Title | Equation | Description | Further Reading |
|---|---|---|---|
| Distance Calculation using Parallax |  Equation 10 - Distance Calculation using Parallax | The distance to an object in parsecs is equal to 1 AU over the parallax in arc seconds. | |
| Angular Size Calculation |  Equation 12 - Angular Size Calculation | Calculate the angular size of an object based on its apparent size and distance between measure and observer, where theta is the angular size in radians, Sap is the apparent size in mm and l is the distance between the measure and the observer. |
Magnitude Equations
| Title | Equation | Description | Further Reading |
|---|---|---|---|
| Pogsons Relation |  Equation 20 - Pogsons Relation | Pogson's Relation is used to find the magnitude difference between two objects expressed in terms of the logarithm of the flux ratio | |
| Absolute Magnitude Relation |  Equation 23 - Absolute Magnitude Relation | Very similar to Pogsons Relation for apparent magnitudes, this equation shows the relation for absolute magnitudes. | |
| Distance Modulus |  Equation 25 - Distance Modulus | Distance modulus can be used to find a relationship between a stars absolute magnitude and its apparent magnitude given a distance, d, in parsecs. | How Do We Measure Distance in Space Using Parallax and Parsecs |
| Absolute Magnitude |  Equation 31 - Absolute Magnitude | Calculating the Absolute Magnitude of a star within our galaxy. | |
| Bolometric Magnitude |  Equation 39 - Bolometric Magnitude | Bolometric magnitude is related to the luminosity ratio | |
| Luminosity ratio of magnitudes |  Equation 40 - Luminosity ratio of magnitudes | ||
| Distance Modulus solved for d |  Equation 63 - Distance Modulus solved for d |
Gravity & Orbits Equations
| Title | Equation | Description | Further Reading |
|---|---|---|---|
| Kepler's Laws of Planetary Motion |  Equation 2 - Kepler's Laws of Planetary Motion | Keplers law of Planetary Motion is simple and strait forward: The squares of the orbital periods of planets are directly proportional to the cubes of the semi-major axis of their orbits. | |
| Gravitational interaction |  Equation 43 - Gravitational interaction | Gravitational interaction is the most important force, and so the most useful definition of the potential energy. For two-body problems, potential energy, U, is given by this formula. | The Physics Governing the Universe - Interactions, EM, Gravity |
| Centripetal force |  Equation 44 - Centripetal force | An orbiting body, at radius r, experiences the centripetal force Fc, which keeps it moving in a circle. | The Physics Governing the Universe - Interactions, EM, Gravity |
| Gravitational force |  Equation 45 - Gravitational force | The Physics Governing the Universe - Interactions, EM, Gravity | |
| Schwarzschild radius |  Equation 50 - Schwarzschild radius | The Schwarzschild radius is the radius of a sphere such that, if all the mass of an object were to be compressed within that sphere, the escape velocity from the surface of the sphere would equal the speed of light. | What Are Black Holes? Black Holes Explained - From Birth to Death |
Energy Equations
| Title | Equation | Description | Further Reading |
|---|---|---|---|
| Energy of a Photon |  Equation 29 - Energy of a Photon | The energy of a photon in Joules is equal to h (Planck constant) times by its frequency. | |
| Frequency of Light |  Equation 30 - Frequency of Light | The frequency of light is dependant on the speed of light (c) and it's wavelength. | |
| Kinetic energy of a particle |  Equation 42 - Kinetic energy of a particle | The fundamental definition of the kinetic energy of a particle is given by the formula, where v is the velocity of the particle | The Physics Governing the Universe - Interactions, EM, Gravity |
| The energy of a photon |  Equation 46 - The energy of a photon | The energy, E, of a photon where h is Planck's constant, v is the frequency of the wave, c is the speed of light and λ is the wavelength. | |
| Normal gas pressure |  Equation 49 - Normal gas pressure | What is Electron Degeneracy Pressure and White Dwarfs Explained |
Time Equations
| Title | Equation | Description | Further Reading |
|---|---|---|---|
| Local Sidereal Time |  Equation 14 - Local Sidereal Time | Use this formula to calculate local sidereal time given the Greenwich sidereal time plus your longitude (east of Greenwich) | |
| Relationship between LST, HA and RA |    Equation 17 - Relationship between LST, HA and RA | These equations show the relationsip between Local Sidereal Time, Hour Angle and Right Ascension. |
Solar Physics Equations
| Title | Equation | Description | Further Reading |
|---|---|---|---|
| Ratio of Fluxes |  Equation 18 - Ratio of Fluxes | Ratio of flux between two stars with apparent magnitudes m and n and measured fluxes of Fm and Fn. | |
| Luminosity and Flux |  Equation 22 - Luminosity and Flux | This equation shows the relationship between the observed flux of a star and its luminosity. | |
| Inverse Square Law for Flux |  Equation 24 - Inverse Square Law for Flux | This equation gives a stars absolute flux (FM) using the inverse square law for a star at distance d (parsecs), with observed flux Fm. | |
| Stefan-Boltzmann Law |  Equation 26 - Stefan-Boltzmann Law | Also known as Stefan's law, states that the total energy radiated per unit surface area of a black body in unit time, is directly proportional to the fourth power of the black body's thermodynamic temperature T. | |
| Electron degeneracy pressure |  Equation 38 - Electron degeneracy pressure | Electron degeneracy pressure in a material can be computed, where h is Planck's constant, me is the mass of the electron, mp is the mass of the proton, ρ is the density, and μe = Ne / Np is the ratio of electron number to proton number. | What is Electron Degeneracy Pressure and White Dwarfs Explained |
| Wien's Displacement Law |  Equation 61 - Wien's Displacement Law |
Cosmology Equations
| Title | Equation | Description | Further Reading |
|---|---|---|---|
| Redshift |  Equation 27 - Redshift | Redshift calculation based on observed wavelengths. | Redshift and Blueshift Explained - How We Know Disance to Far-Off Objects |
| Temperature scale factor |  Equation 32 - Temperature scale factor | Temperature of the universe through time as a function of scale factor. | Expansion of the Universe, Cosmic Scale Factor and Hubble's Law |
| Temperature redshift. |  Equation 33 - Temperature redshift. | Temperature of the universe expressed as a function of redshift. T0 represents the temperature of the universe today (~2.7K). | Redshift and Blueshift Explained - How We Know Disance to Far-Off Objects |
| Proper Distance |  Equation 35 - Proper Distance | Proper distance x(t) corresponding to different epochs in terms of the comoving radial distance coordinate r. | Redshift and Blueshift Explained - How We Know Disance to Far-Off Objects |
| Redshift and Scale Factor |  Equation 36 - Redshift and Scale Factor | Relationship between redshift and scale factor for another epoch. | Redshift and Blueshift Explained - How We Know Disance to Far-Off Objects |
| Hubble's Law |  Equation 47 - Hubble's Law | The linear relationship between recession velocity, v, and the distance, x, of a local galaxy | Expansion of the Universe, Cosmic Scale Factor and Hubble's Law |
| Planck's Law of Blackbody Radiation | 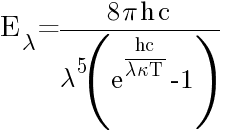 Equation 58 - Planck's Law of Blackbody Radiation | Formula to determine the spectral energy density of the emission at each wavelength (Eλ) at a particular absolute temperature (T). | |
| Wien's Displacement Law |  Equation 59 - Wien's Displacement Law | The frequency of the peak of the emission (fmax) increases linearly with absolute temperature (T) | |
| Stefan-Boltzmann Law |  Equation 60 - Stefan-Boltzmann Law | Relates the total energy emitted (E) to the absolute temperature (T). |
Relativity Equations
| Title | Equation | Description | Further Reading |
|---|---|---|---|
| Special theory of relativity |  Equation 41 - Special theory of relativity | The special theory of relativity states that mass and energy are equivalent. | The Physics Governing the Universe - Interactions, EM, Gravity |
| Lorentz factor |  Equation 48 - Lorentz factor | The factor by which time, length, and relativistic mass change for an object while that object is moving. |






