What is Black Body Radiation?All objects are continually absorbing and emitting infrared radiation. Black bodies are perfect absorbers and emitters of radiation.
All objects with a temperature above absolute zero (0 K, -273.15 ° C) emit energy in the form of electromagnetic radiation.
The intensity of radiation increases as the body gets hotter and gives out more radiation in a given time. The type of radiation emitted also changes with temperature. The spectral distribution of the thermal energy radiated by a blackbody (i.e. the pattern of the intensity of the radiation over a range of wavelengths or frequencies) depends only on its temperature.
A black body is a theoretical or model body which absorbs all radiation falling on it, reflecting or transmitting no energy at any wavelength. It is a hypothetical object which is a "perfect" absorber and a "perfect" emitter of radiation over all wavelengths.
There are no known objects that are perfect at absorbing or emitting all radiation of every possible frequency that may be directed at it. Some objects do, however, come close to this and these are referred to as black bodies.
Stars are considered to be black bodies because they are very good emitters of most wavelengths in the electromagnetic spectrum. This suggests that stars also absorb most wavelengths. Whilst there are a few wavelengths that stars do not absorb or emit, this figure is very low, so they can be treated as black bodies. Planets and black holes are also treated as nearly perfect black bodies.
The characteristics of blackbody radiation can be described in terms of several laws:
Planck's Law of Blackbody Radiation
A formula to determine the spectral energy density of the emission at each wavelength (Eλ) at a particular absolute temperature (T).
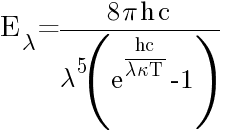
Equation 58 - Planck's Law of Blackbody Radiation
Planck radiation is said to be thermal radiation, such that the higher the temperature of a body the more radiation it emits at every wavelength.
Planck radiation has a maximum intensity at a wavelength that depends on the temperature of the body. For example, at room temperature (~300 K), a body emits thermal radiation that is mostly infrared and invisible. At higher temperatures, the amount of infrared radiation increases and can be felt as heat, and more visible radiation is emitted so the body glows visibly red. At higher temperatures, the body is bright yellow or blue-white and emits significant amounts of short-wavelength radiation, including ultraviolet and even X-rays. The surface of the sun (~6000 K) emits large amounts of both infrared and ultraviolet radiation; its emission is peaked in the visible spectrum. This shift due to temperature is called Wien's displacement law.
Wien's Displacement Law
This law states that the frequency of the peak of the emission (fmax) increases linearly with absolute temperature (T). Conversely, as the temperature of the body increases, the wavelength at the emission peak decreases.

Equation 59 - Wien's Displacement Law
Formally, Wien's displacement law states that the spectral radiance of black body radiation per unit wavelength, peaks at the wavelength λmax given by:

Equation 61 - Wien's Displacement Law
Stefan-Boltzmann Law
Stefan-Boltzmann Law relates the total energy emitted (E) to the absolute temperature (T).

Equation 60 - Stefan-Boltzmann Law
The temperature of stars other than the Sun can be approximated using a similar means by treating the emitted energy as black body radiation. So:

Equation 26 - Stefan-Boltzmann Law
Where L is the luminosity, σ is the Stefan-Boltzmann constant, R is the stellar radius and T is the effective temperature.
This same formula can be used to compute the approximate radius of a main sequence star relative to the sun.

Equation 62 - Stefan-Boltzmann Law and Star Size
Where R⊙ is the solar radius, L⊙ is the solar luminosity, and so forth.
Black Body Curves
Bodies emit a continuous range of electromagnetic radiation at different energy values. This means that the radiation that is emitted is spread out over a range of different frequencies and wavelengths.

In the image above we can see that the black body radiation curves have quite a complex shape which is described by Planck's Law. The spectral profile (curve) at a specific temperature corresponds to a specific peak wavelength, and vice versa. As the temperature of the blackbody increases, the peak wavelength decreases as per Wien's Law. The intensity (or flux) at all wavelengths increases as the temperature of the blackbody increases. The total energy being radiated (the area under the curve) increases rapidly as the temperature increases according to Stefan-Boltzmann Law.
Although the intensity may be very low at very short or long wavelengths, at any temperature above absolute zero energy is theoretically emitted at all wavelengths (the black body radiation curves never reach zero).
In astronomy, stars are often modelled as blackbodies, although it is not always a good approximation. The temperature of a star can be deduced from the wavelength of the peak of its radiation curve.
In 1965, the cosmic microwave background radiation (CMBR) was discovered by Penzias and Wilson, who later won the Nobel Prize for their work. The radiation spectrum was measured by the COBE satellite and found to be a remarkable fit to a blackbody curve with a temperature of 2725 K and is interpreted as evidence that the universe has been expanding and cooling for about 13.7 billion years. A more recent mission, WMAP, has measured the spectral details to a much higher resolution, finding tiny temperature fluctuations in the early Universe which ultimately led to the large-scale structures we see today.









